Dr. Michael Schwarz M.Sc.

Supervisory committee: | |
|---|---|
| Prof. Dr. Bernd Henning, opens an external URL in a new window | |
| |
| Final exam: | |
| March 11, 2022 | |
Supervisory committee: | |
| Prof. Dr. Bernd Henning, opens an external URL in a new window | |
| |
| Final exam: | March 11, 2022 |
This thesis deals with the ultrasound-based measurement and reconstruction of temperature fields and the possible application of this method in bioreactors. Due to the temperature dependence of the speed of sound, the average temperature along a path of known length between a transmitter and a receiver can be determined from the travel time of ultrasound. If the ultrasonic travel time is measured along a sufficiently large number of paths in a slice plane, this enables the reconstruction of the distribution of the speed of sound and, subsequently, the calculation of the temperature field in this plane. For this, however, an ill-posed inverse problem has to be solved. This requires suitable reconstruction algorithms.
In this thesis, important principles of ultrasound-based temperature measurement as well as of the solution of inverse problems are summarized. A measurement setup is then presented in which 16 ultrasonic transducers are attached at regular intervals along the circumference of a round, water-filled basin. However, the number of useable direct measuring paths is limited by the transducers' small radiation angle. Therefore, additional paths with backscattering on the opposite basin wall are considered. With the measurement setup described, the travel times of ultrasonic wave packages are measured, which are used to reconstruct the temperature field inside the basin. The travel time measurement is also simulated for various assumed temperature distributions.
 Figure 1: Possible direct measurement paths (gray) and paths with backscattering (black).
Figure 1: Possible direct measurement paths (gray) and paths with backscattering (black).
Two different methods are utilized to reconstruct the temperature distribution from the measured or simulated travel times. The first method is the Tikhonov regularization, which is widely used for solving inverse problems. The second method comes from compressed sensing and minimizes the total variation of the solution vector. This method can be applied if the temperature field can be transformed into a sparse representation. This is the case if the temperature field deviates from an otherwise approximately constant value only in locally limited areas. Both methods yield good reconstruction results. For temperature fields with only small deviations, measurement uncertainties of less than 0.5 K are achieved. If the condition for its applicability is met, the minimization of the total variation leads to better results in all cases considered.
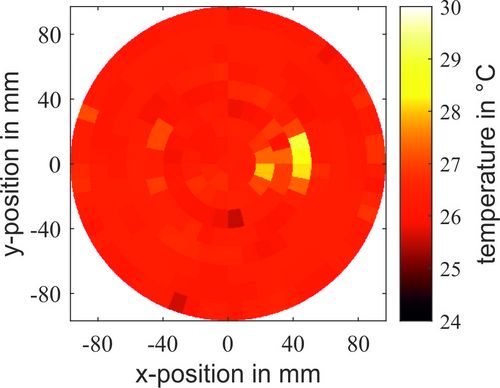 Figure 2: Result of reconstructing a temperature field from measured data by minimizing the total variation.
Figure 2: Result of reconstructing a temperature field from measured data by minimizing the total variation.
Keywords: temperature measurement, temperature field, ultrasonic travel time measurement, tomographic reconstruction, Tikhonov regularization, compressed sensing
 Go to JKU Homepage
Go to JKU Homepage


