Am 11. November ist der bolivianische Präsident Evo Morales nach anhaltenden Massenprotesten auf Druck des Militärs zurückgetreten. Einer der Gründe für die Proteste waren Vorwürfe über Betrügereien bei den im Oktober abgehaltenen Wahlen, bei denen Morales den erforderlichen Abstand von 10 Prozentpunkten zum Gegenkandidaten knapp erreichte.

Die Organisation Amerikanischer Staaten hatte daraufhin eine Untersuchung eingeleitet, die auf Basis der Wahlergebnisse und der zugehörigen Zeitstempel zum Schluss kam, dass das Ergebnis statistisch unwahrscheinlich sei, und empfahl deshalb eine Neuwahl.

Bemerkenswert war hierbei die Verwendung statistischer Verfahren zur Entscheidungsfindung – welch Gegensatz zu unseren letzten Präsidentschaftswahlen!

Die am 22. Mai 2016 stattgefundene Stichwahl zwischen Norbert Hofer und Alexander van der Bellen, welche Letzterer mit etwa 30.000 Stimmen Vorsprung gewann, wurde ja nach Einspruch der FPÖ vom Verfassungsgerichtshof aufgehoben. Dieser hatte 11 Wahlbezirke identifiziert, für welche nicht ausgeschlossen werden konnte, dass die darin abgegebenen Briefwahlstimmen manipuliert worden waren. Der VfGH argumentierte in seinem Erkenntnis allein mit der prinzipiellen Möglichkeit, dass der Wahlausgang dadurch beeinflusst hätte sein können, ohne jedoch die vorliegenden Daten heranzuziehen.

Der Statistiker Erich Neuwirth von der Universität Wien aber untersuchte unter der Annahme eines über die Wahlkreise durchschnittlich konstanten Verhältnisses von Urnen- zu Briefwahlstimmen, die sogenannten Residuen, das heißt die Abweichungen der Daten vom zugrundegelegten Modell. Bei eventuell vorliegenden Manipulationen hätten sich diese Residuen in den beanstandeten Wahlkreisen in statistisch signifikanter Weise, das heißt über die natürlichen zufälligen Schwankungen hinaus, von denen in den restlichen 106 Wahlkreisen unterscheiden müssen.

Dies war allerdings nicht im Geringsten der Fall. Zusätzlich lässt sich über die Residuen die Wahrscheinlichkeit dafür bestimmen, dass es trotz allem zu einer ergebnisverändernden Manipulation gekommen wäre. Neuwirth und Walter Schachermayr beziffern diese in einem Artikel in der österreichischen Zeitschrift für Statistik mit 1 zu 7,56 Milliarden, also etwa einem Tausendstel der Chance auf einen Lottosechser.

In einer unabhängigen, auch residuenbasierten Analyse kam Walter Mebane, Statistikprofessor an der University of Michigan, zu ähnlichen, in der „Washington Post“ der breiten Öffentlichkeit vorgelegten Schlussfolgerungen. Warum wurden diese harten Fakten vom Verfassungsgerichtshof nicht berücksichtigt, ja womöglich gar nicht in Erwägung gezogen? Darüber kann nur gemutmaßt werden, denn Indizien mit Wahrscheinlichkeitsangaben werden ja in anderen Verfahren durchaus benutzt, man denke nur an DNA-Vergleiche.

Aber schon 2016 haben ich im „Standard“ und Neuwirth und Schachermayr im „Falter“ festgestellt, dass möglicherweise in der Höchstrichterschaft, aber auch in der Bevölkerung im Allgemeinen, das Bewusstsein für statistische Fragestellungen kaum vorhanden ist. Dabei wird die „statistical literacy“ – also die Daten-Alphabetisierung – häufig als Schlüsselkompetenz des 21. Jahrhunderts genannt. Und nur wer Daten lesen und verstehen kann, wird in einer Welt der Daten Vertrauen in die Demokratie haben. Diese Kolumne besteht auch in der Hoffnung, zur Verbreitung dieser „data literacy“ beizutragen.

JKU: PLATZ FÜR FAKTEN STATT FAKES  

Auf der Webseite https://neuwal.com/wahlumfragen werden Ergebnisse von Wahlumfragen in Österreich dokumentiert. In den letzten 25 unabhängigen Wahlumfragen vor der Nationalratswahl 2017 lag die ÖVP, damals noch Juniorpartner der SPÖ in der Regierung, mit ihrem Anteil konstant zwischen 32 und 34 Prozent (siehe 1. Abbildung).

Während dieser Umstand in der breiten Öffentlichkeit wohl so wahrgenommen wird, dass sich in der Gesamtbevölkerung in diesem Zeitraum offenbar nichts getan hat, schrillen bei Sachkundigen die Alarmglocken. Denn auch wenn sich in der Population absolut nichts ändert, unterliegen selbst nach den Regeln der Survey-Statistik durchgeführte Erhebungen einer natürlichen Stichprobenschwankung. Durch die Zufälligkeit der Auswahl der Stichprobenelemente lässt sich dann aber die Ungenauigkeit der Resultate auf Basis der Wahrscheinlichkeitstheorie bestimmen.

Geht man vom Idealfall im Hinblick auf die Genauigkeit aus, also davon, dass es sich um 25 unabhängige einfache Zufallsstichproben ohne Nonresponse gehandelt hat (denn sonst könnten die Ergebnisse womöglich noch stärker streuen), dann kann z. B. bei angenommenen konstanten 33 Bevölkerungsprozenten die Wahrscheinlichkeit dafür bestimmt werden, dass trotz der Stichprobenschwankung zufällig diese konstanten Ergebnisse von gerundeten 32 bis 34 Prozent für die ÖVP zu Stande gekommen sind. Dies besitzt eine Wahrscheinlichkeit von 0,00000411. Das bedeutet, dass eine solche Konstanz von 25 Umfragen durch Zufall im Schnitt nur jedes 1 : 0,00000411 ≈ 240.000-ste Mal passieren wird. So unwahrscheinlich ist es selbst unter Idealbedingungen, dass 25 unabhängige Stichproben für eine Partei immer 32 bis 34 Prozent ergeben, wenn der Populationswert 33 Prozent beträgt!

Ein beliebiger zufälliger Verlauf, der sich an die Gesetzmäßigkeiten der Wahrscheinlichkeitstheorie hält, wäre zum Vergleich etwa jener in der 2. Abbildung. Sehen Sie den Unterschied zu den veröffentlichten Wahlumfragen?

Wieso gleichen sich die berichteten Umfrageergebnisse also so stark, wenn es äußerst unwahrscheinlich ist, dass sie es zufällig tun? Sind diese Umfragen womöglich gar keine Umfragen, sondern „Unfragen“?  

Trinken Sie gerne Tee? In unseren Breiten selten mit Milch, oder? Aber wenn doch, dann Milch zuerst in die Tasse oder umgekehrt? Sie denken, das macht keinen Unterschied? Auch der junge Ronald Fisher (später zum Säulenheiligen der Statistik avanciert) dachte das, als er Muriel Bristol einst eine frisch aufgegossene Tasse Tee anbot und diese mit dem Hinweis ablehnte, es schmecke ihr besser, wenn die Milch zuvor hinzugefügt würde. Dies geschah an einem Nachmittag in den frühen 1920er Jahren an der Agrarforschungsstation in Rothamsted, an der die beiden beschäftigt waren. Der genaue Tag ist nicht bekannt, aber die Uhrzeit war 16.00 Uhr, zur in Rothamsted rituell eingehaltenen Teepause.

Die Algenforscherin Bristol wird Ihnen möglicherweise unbekannt sein, aber als „The Lady Tasting Tea“ ist sie durch diese Teepause in die Wissenschaftsgeschichte eingegangen. Fisher nämlich, der ihre Behauptung, sie könne unterscheiden, ob der Tee oder die Milch zuerst in die Tasse gegossen wurde, nicht glauben wollte, entschloss sich, diese mit einem Experiment zu überprüfen. Dieser Versuch, welchen Fisher später in seinem berühmten, 1935 erschienenen Buch „The Design of Experiments“ beschreibt, gilt als der Geburtsmoment der statistischen Versuchsplanung und quasi als Vorbild für die Standardvorgehensweise in allen experimentellen Wissenschaften.

Was war Fishers bahnbrechender Vorschlag? Er ließ vier Tassen zuerst mit Tee (T) und vier Tassen zuerst mit Milch (M) füllen und präsentierte diese Dr. Bristol in zufälliger Reihenfolge. Nur wenn Bristol in der Lage wäre, alle davon korrekt zu identifizieren, würde er ihr die behauptete Fertigkeit zugestehen. Was auf den ersten Blick wie ein unspektakulärer Vorschlag aussieht, bereitete die Grundlage für in der Statistik nunmehr unbestrittene Versuchsprinzipien wie Randomisierung, Replikation sowie Balance und führte gleich nebenher das exakte statistische Testen ein. In seinem brillanten, nur neun Seiten langen und 1956 erschienenen Artikel „Mathematics of a Lady Tasting Tea“ erklärt Fisher einleuchtend (und ohne Verwendung von Formeln), welche Abweichungen von seiner Versuchsanordnung welche negativen Konsequenzen hätten.

Hauptsächlich ging es dabei natürlich darum, möglichst auszuschließen, dass Dr. Bristol einfach durch Raten zum richtigen Ergebnis gelangte. Nun, bei jeweils vier Tassen können sich verschiedene zufällige Anordnungen ergeben. Die Wahrscheinlichkeit, bei diesem Versuch durch pures Raten immer Recht zu haben, beträgt daher etwa 1,4 %, was für Fisher ausreichend unwahrscheinlich wäre, um als zufällig zu gelten (die bekannte 5%-Signifikanzhürde geht auch auf ihn zurück).

Man bemerke, dass hiermit nicht nur der Permutationstest, sondern auch der sogenannte p-Wert eingeführt wurde, Konzepte, welche heute in den experimentellen Anwendungen entscheidende Bedeutung haben, insbesondere zum Beispiel bei klinischen Tests von Medikamenten oder Behandlungsverfahren.

Ob Frau Bristol den Test bestanden hat, ist übrigens nicht ganz geklärt. Herr Fisher verliert in seinen Schriften kein Wort darüber, Zeugen der berühmten Teepause sind eher auf Bristols Seite.

JKU: PLATZ FÜR FAKTEN STATT FAKE NEWS  

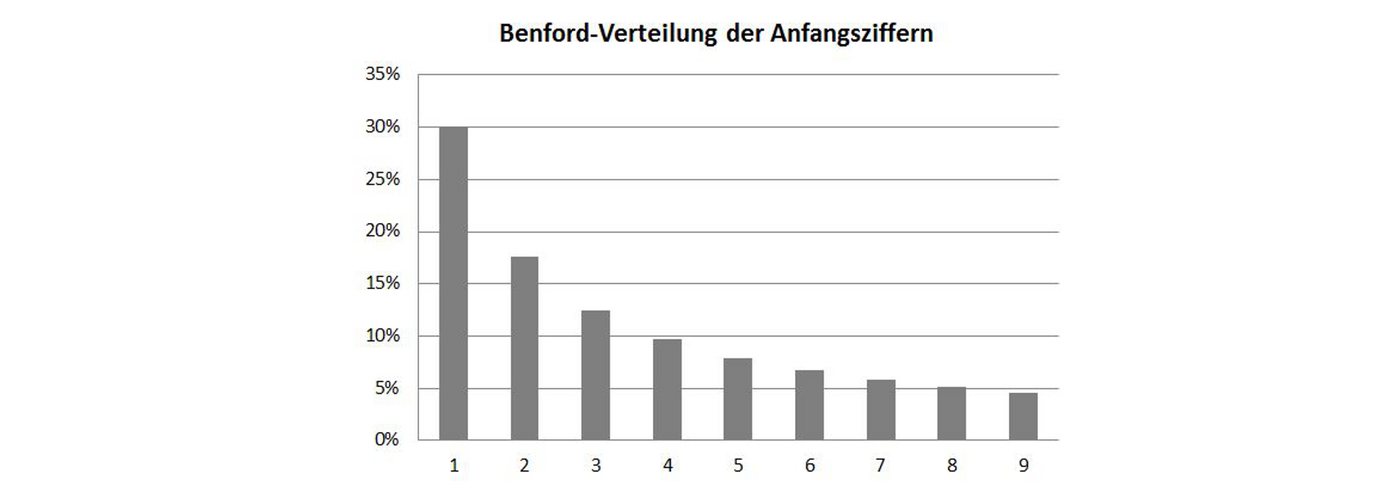
Nehmen wir mal an, Sie wollen Ihr Finanzamt bei Ihrer Steuererklärung betrügen. Nicht, dass wir das von Ihnen vermuten würden, aber wenn doch, dann sollten Sie beim Ausfüllen der Formulare mit irgendwelchen Fantasiezahlen vorsichtig sein. Verwenden Sie dabei nämlich, was viele als naheliegend und vernünftig annehmen, alle Ziffern gleichmäßig, so lassen sich Ihre numerischen Angaben relativ einfach als Fälschungen identifizieren. Das kommt von einem erstaunlichen Umstand, welcher in der Statistik nach seinen Entdeckern (Newcomb)- Benford-Gesetz genannt wird und zur Folge hat, dass etwa Zahlen mit führenden Einsen in vielen Zusammenhängen öfter vorkommen als solche mit führenden Zweien, mit führenden Zweien wiederum öfter als mit führenden Dreien und so fort. Genauer gesagt tritt nach diesem Gesetz eine Zahl mit Ziffer z an erster Stelle mit einer zu erwartenden Häufigkeit log10(1+1/z) auf. Die Eins tritt demnach in etwa 30 % aller Fälle auf, die Zwei in ca. 18 % und so weiter. (vgl. etwa: https://de.wikipedia.org/wiki/Benfordsches_Gesetz)

Für das Auftreten dieser speziellen Verteilung lassen sich vielerlei Erklärungen finden. Am eingängigsten ist vielleicht jene über einen gleichmäßigen Wachstumsprozess. Pflanzen Sie etwa einen ein Meter hohen Baum, welcher monatlich im Schnitt mit einem konstanten Faktor, sagen wir 1 %, wächst, dann dauert es 70 Monate, bis dieser Baum zwei Meter hoch ist, weitere 41 Monate, bis er drei Meter misst und so weiter. Bei einer Höhe von neun Metern dauert es nur noch elf Monate bis zur Höhe von zehn Metern und dann steht wieder eine Eins am Anfang und der Prozess setzt sich fort. Natürlich wachsen Bäume, in der Realität nicht gleichmäßig und schon gar nicht unbeschränkt, aber betrachtet man eine größere Anzahl unterschiedlich alter Bäume spielt dies keine Rolle. Andere Beispiele für Benford-verteilte Zahlen sind Hausnummern oder Bevölkerungsgrößen. Das Phänomen ist allerdings nicht auf spezifische Datensätze beschränkt.

Machen Sie selbst einen Versuch: Nehmen Sie eine größere Kollektion von Daten aus Ihrem Umfeld, z. B. Ihren Forschungen, die nicht zu klein ist und bei welcher der Datenbereich nicht auf eine bestimmte Zahl von Stellen beschränkt ist, ordnen Sie die Werte nach der führenden Ziffer und zählen Sie: Sie werden staunen (oder jetzt vielleicht nicht mehr).

Das Benford-Gesetz lässt sich übrigens auf weitere Stellen der untersuchten Zahlen erweitern, allerdings mit abnehmender Ungleichmäßigkeit. Die letzten Ziffern sollten, wie man sich leicht überlegen kann, mit jeweils gleicher, also je 10 % Häufigkeit auftreten.

Das Fälschen einer Steuererklärung erfordert also wesentlich mehr statistisches Know-how, als man vermuten möchte. Von 100 einzutragenden Zahlen sollten rund 30 mit einer Eins, rund 18 mit einer Zwei, und so fort beginnen. Aber auch die zweiten Stellen sollten sich nach den entsprechenden Regeln für die zweiten Ziffern richten. Und die dritten gegebenenfalls nach jenen für die dritten … In der Praxis werden Verletzungen der Benford’schen Verteilung übrigens nicht nur zum Aufdecken von Wirtschaftskriminalität, sondern auch etwa von Genanomalitäten oder Wahlbetrug verwendet.

JKU: PLATZ FÜR FAKTEN STATT FAKE NEWS

Das EU-Sommerzeit-Nichtreferendum

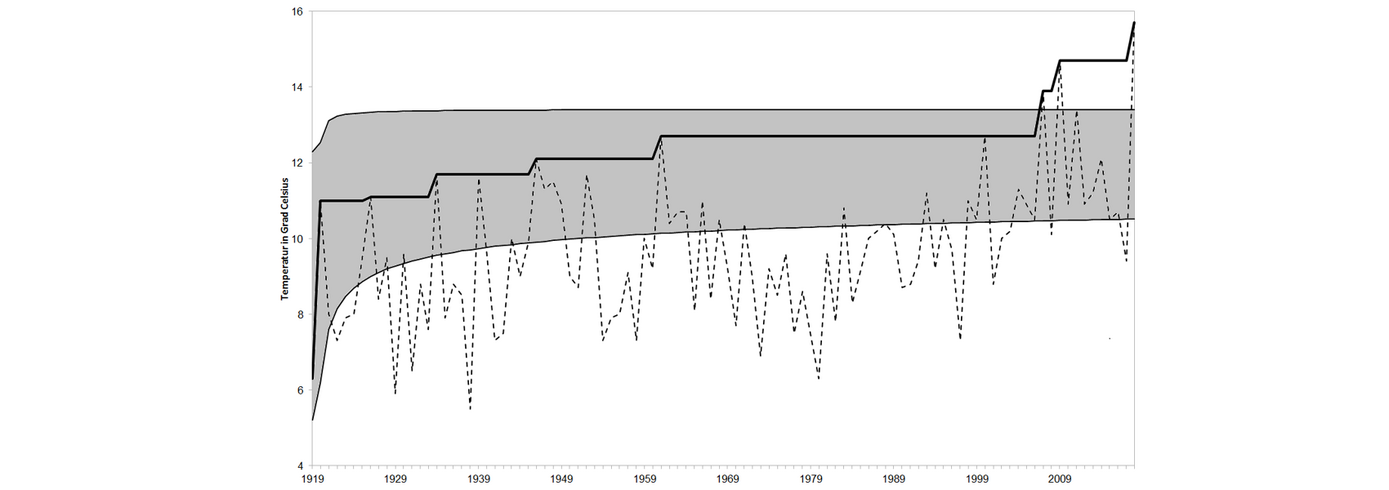
2017 war eines der drei wärmsten Jahre, der April 2018 der wärmste, der darauf folgende Mai der heißeste seit Messbeginn – ein Rekord jagt den anderen.

Know your status, but know your probability too!
 

Wie gelingt es Prozentzahlen, dass die Grenze zwischen Fakten und Fake News verschwimmt?